关于卡常数,OI界一直有着各种奇妙的传言,比如:
+=比=慢*(a + i)比a[i]快x * 10比(x << 1) + (x << 3)慢- 循环中,
++i比i++快- 循环变量加上
register快std::pair <T1, T2>很慢std::min和std::max很慢if ... else ...比...?...:...慢
卡常的一套理论
说实话,现在很多人卡常是跟着感觉走,比如“感觉这样会快点”,最后甚至可能弄出卡了一下午,最后反而变慢了的笑话。
卡常不是玄学,卡常有一套理论在里面,首先我们来学习一些关于计算机内部的东西。
存储器层次结构
基本属性
现代计算机的存储器层次相当奇妙,不过大体是基于一个事实:越快的存储器的单位容量价格越高。
比如,用来制造 CPU 高速缓存的 SRAM 的访问时间只需 1.3ns ,但其价格高达 25 $/MB。
而速度比较捉鸡的 HDD ,价格低至 0.03 $/MB ,但其访问时间达到 3ms(慢的一批)。
尽管各式存储器( SRAM, DRAM, SSD, HDD )价格一直在降低,可它们之间的差距是短时间无法弥补的。
同时,历史数据显示,CPU 的速度从 1985 年到 2015 年翻了 2000 倍,而存储器的发展却落后于 CPU。
由此,我们可以脑补出存储技术的一些属性:不同存储技术的访问时间差异很大,速度较快的技术单位容量价格比速度较慢技术的价格高,而且容量较小。CPU与主存的速度差距在不断拉大。
另一方面,是计算机软件的一些属性:编写良好的计算机软件通常具有良好的时空局部性。
存储器层次结构
为了合理组织存储器,人们研究了一套理论:
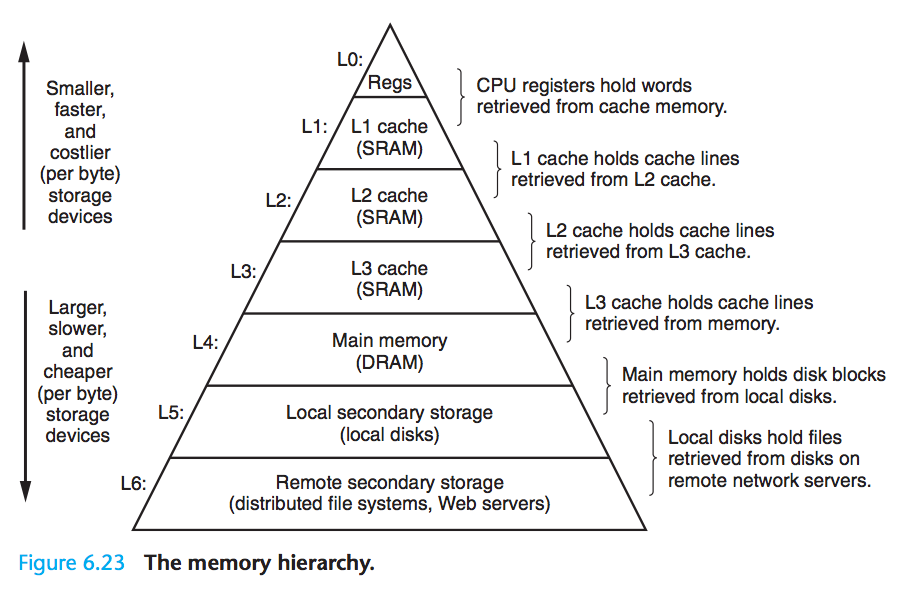
从高到低,存储设备变得更慢,更大,更便宜。
考虑到程序的时空局部性,我们可以在第 $k$ 层里缓存一部分第 $k+1$ 层的数据,从而提高运行效率。
这是相当常见的操作,浏览器会把一些 CSS/JS/HTML 缓存到你电脑的磁盘上,而你的浏览器在运行前需要先从硬盘加载到内存里(虚拟内存,挖坑) ,而你的浏览器在访问内存时,CPU 会把部分内存页缓存到高速缓存里。
下面是一个小表格,描述了各种存储器的性能和信息:
| 类型 | 缓存什么 | 缓存在何处 | 延迟(CPU 周期) | 由谁管理 |
|---|---|---|---|---|
| 寄存器 | 4⁄8 字节 | 芯片上的寄存器 | 0 | 编译器 |
| L1 高速缓存 | 64 字节块 | 芯片上的 L1 高速缓存 | 4 | 硬件(反正你控制不了) |
| L2 高速缓存 | 64 字节块 | 芯片上的 L2 高速缓存 | 10 | 硬件(同上) |
| L3 高速缓存 | 64 字节块 | 芯片上的 L3 高速缓存 | 50 | 硬件(同上) |
| 虚拟内存 | 4KB页 | 主存(内存) | 200 | 硬件 + OS |
(CPU 周期:CPU 频率的倒数)
程序的机器级表示
不学汇编卡什么常
我们要学的是x86-64,也就是俗称的x64。
这时候可能会有疑问,难道汇编还有好几种吗?因为汇编本质上与 CPU 的架构有关,如果指令集不一样,自然用的不是一种汇编。比如某评测鸭使用的竟然是 32 位的操作系统(8012年了),我在本机上xjb写的汇编在上面频频 RE,WA,原因就是指令集架构不同。
寄存器
x86-64的寄存器充分体现了它的历史遗迹:

从图中我们可以看到,%rxx的寄存器都是 64 位的,%exx的都是 32 位的。
操作数指示符
指令总要去操作点什么,x86-64中,操作数可以有三种,分别是:立即数(字面值常量),寄存器,内存引用。
立即数的表示非常简单,通常用$Imm的形式。
寄存器的表示也比较正常,通常用%rxx来表示。
而内存就比较蛇皮了,它的方法异常丰富:
- 绝对寻址:用立即数作为内存地址(相当少见):
Imm,也就是把立即数的$去掉了 - 间接寻址:用寄存器里的值作为内存地址(比如这个寄存器里放了一个指针):
(%rxx),也就是把寄存器用括号括起来 - 基址+偏移量寻址:用寄存器里的值加上一个立即数作为内存地址:
Imm(%rxx),得到的结果是Memory[%rxx + Imm] - 比例变址寻址
(这个名字听起来很牛逼):Imm(%rxx, %ryy, s),得到的结果是Memeory[Imm + %rxx + %ryy * s],其中,比例因子 $s$ 只能是 $1,\ 2,\ 4,\ 8$
比例变址寻址可能比较难懂,最重要的是,我们不知道它能干啥。事实上,比例变址寻址的使用是相当广泛的,在引用数组元素时,它是相当有用的。
同时,比例变址寻址的很多部分都可以省略,比如 $s$ 可以省略,Imm可以省略,甚至连%rxx都可以省略。
常见指令
mov S D,作用:S -> Dlea S D,作用:&S -> Dinc D,作用:D + 1 -> Ddec D,作用:D - 1 -> Dneg D,作用:-D -> Dadd S D,作用:D + S -> Dsub S D,作用:D - S -> Dimul S D,作用:D * S -> Dxor S D,作用:D ^ S -> Dsal k D,作用:D << k -> Dsar k D,作用:D << k -> D(算术右移)shr k D,作用:D << k -> D(逻辑右移)
优化程序性能
说了一大坨,究竟和我卡常有什么关系呢?(抓捕卡常和我存储器有什么关系)我们这就来看看。
编译器的优化
吸一口纯氧
由于 C/C++ 并不要求函数的副作用,所以编译器优化时难免畏首畏尾,生怕把你的程序给优化坏了(反观Haskell,函数都是纯的)。所以这就需要我们花费更多精力,使得编译器生成更好的代码。
优化的思路
减少过程调用
由于过程调用需要对参数进行压栈之类的操作,而栈在内存里,根据我们刚刚学到的知识,访问内存的延迟是很高的,调用过程的开销比较大。在不开优化的情况下,减少过程调用可以显著提高速度。
具体操作可以使用#define或者inline。
消除不必要的内存引用
比如某dalao在写树状数组的时候写了这样的代码:
#define Lowbit(x) (x&-x)
void Change2(register int k,const int & x) {
while (k > 0) {
f[k] += x;
k -= Lowbit(k);
}
}
值得注意的是,这个函数的第二个参数const int & x使用了引用。尽管在语言层面上,引用和指针没啥关系,但是在实现上,引用即指针,既然是指针,引用的肯定是内存里的东西。这下好了,本来这个参数是可以通过寄存器传递的,现在还要从内存里把它读出来,速度肯定不会理想。
循环展开
不建议手写这个东西,开个优化,编译器会无私地帮助你的。
编写高速缓存友好的代码
提高时空局部性
提高时间与空间局部性即可使你的程序对高速缓存友好。
比如我之前写的树剖,上来先开一大堆数组:
int siz[maxn], top[maxn], son[maxn], fa[maxn], dep[maxn];
而访问的时候,却总是siz[i], top[i]之类的连着访问,这样做空间局部性极差,为了提高运行速度,我们可以把这些东西扔进结构体里,由于结构体内的元素在内存里是按顺序排列的,所以可以提高空间局部性:
struct node
{
int siz, top, son, dep, fa;
node() { siz = top = dep = fa = 0;}
};
node nd[maxn];
值得一提的时,做任何优化前请先做 profile ,优化耗费时间最长的部分往往能带来更大的收益。( gprof 了解一下)
避免使用步长为 $2$ 的 $n$ 次幂的内存引用
由于高速缓存不是全相连的,使用步长为 $2$ 的 $n$ 次幂的内存引用模式会导致每次访问都不命中,效率极低。
做一做实验
我们来验证一下开篇看到的传言
+=与=
测试代码:
int func (int & a, int b) {
a += b;
return a;
}
int func2 (int & a, int b) {
a = a + b;
return a;
}
这两个玩意编译出来一模一样,不管是开不开优化,所以也无所谓哪个快哪个慢了。
值得注意的是,不开优化时,gcc默认使用栈来传递参数,生成的汇编极其难看,如果给两个参数都加上register会好很多
*(a + i)与a[i]
测试代码:
int vec[(int)1e3];
int func (unsigned int idx) {
return vec[idx];
}
int func2 (int idx) {
return vec[idx];
}
int func3 (unsigned int idx) {
return *(idx + vec);
}
int func4 (int idx) {
return *(idx + vec);
}
在不开优化的情况下,func所使用的指令最少,func2比func多了一条ctlq(符号拓展),而func3和func4更是忠诚地复现了代码的操作,没有使用比例变址寻址,指令条数更多。
当然,开了优化之后它们都一样。
x * 10与(x << 1) + (x << 3)
测试代码:
int func(int x) {
return x * 10;
}
int func2(unsigned int x) {
return x * 10;
}
int func3(int x) {
return (x << 1) + (x << 3);
}
int func4(unsigned int x) {
return (x << 1) + (x << 3);
}
在不开优化时,x * 10被编译器优化为((x << 2) + x) + ((x << 2) + x),指令条数和移位版本相同。
在开优化时,x * 10被优化为:
leal (%rdi,%rdi,4), %eax
addl %eax, %eax
即2 * (x + x * 4),指令条数和移位版本还是相同的。
++i与i++
测试代码:
int vec[(int)1e3];
int func (int n) {
int sum = 0;
for (int i = 0; i < n; ++i)
sum += vec[i];
return sum;
}
int func1 (int n) {
int sum = 0;
for (int i = 0; i < n; i++)
sum += vec[i];
return sum;
}
在循环里他们俩编译出来根本一模一样,也就无所谓哪个快,哪个慢了。
register有用吗
测试代码:
int vec[(int)1e3];
int func (register int n) {
int sum = 0;
for (register int i = 0; i < n; ++i)
sum += vec[i];
return sum;
}
int func1 (int n) {
int sum = 0;
for (int i = 0; i < n; i++)
sum += vec[i];
return sum;
}
在不开优化的情况下,gcc默认把所有局部变量和参数放到栈里(所有寄存器是用来吃瓜的吗?),加上register会有一点好处。
在开优化的情况下,能进寄存器的都在寄存器里,加不加都无所谓了。
std::min与手写版本
测试代码:
int mmin (int n, int m) {
if (n < m) return n;
else return m;
}
int mmin2 (int n, int m) {
return (n < m) ? n : m;
}
#include <algorithm>
int mmin3(int n, int m) {
return std::min(n, m);
}
开优化时,这三个都被编译成条件传送的方式,而不开时,mmin与mmin2完全一样,std::min则显得有点蛇皮。由于std::min的声明是std::min(const T & a, const T & b),也就是说,参数是按引用传送的,实际上是一个指针,所以指令与自己手写的相比多了几条。